第2号
農業政策の効果の計量分析
鈴土 靖
鈴土 靖
(会計検査院外務検査課調査官)
会計検査院は,決算が予算執行の状況を正確に表示しているか(正確性),会計経理が予算や法令などに従って適正に処理されているか(合規性),事業が経済的,効率的に実施されているか(経済性・効率性),事業が所期の目的を達成し効果を上げているか(有効性),といった観点から検査を行っている。政府・政府機関等の,会計機関をはじめとする行政機構が成熟してくるにつれ,正確性・合規性に関する問題は減少してきており,自然,会計検査院の検査の主眼も経済性・効率性,有効性へと移行してきている。
ところで,現在行われている経済性・効率性・有効性についての検査のほとんどはミクロ的な視点で行われている。しかも有効性についての検査は,そのほとんどが定性的である。つまり,ある特定の経理や事業を取り上げて,例えば機材の購入や施設の建設において,その購入価格や建設費用が不必要に高額になっていないか,導入された機材や建設された施設は当初の目的どおり,遊休する事なく使用されているか,といった観点から検査を行っているのである。
もっとマクロ的な視点から,しかも定量的に検査ができないだろうか,例えば,農業に対する政府支出が1,000円増大したときの効果は,金額で言えばいくらに当たるのかがわからないだろうか,というのは,会計検査院の人間全員が多少なりとも考えていることであろう。
幸い筆者は筑波大学大学院修士過程への2年間の国内留学という機会を得ることができたので,その機会を利用して多少なりとも勉強してみたが,前述のような分析は,適切なモデルと計量経済学的手法を用いれば,統計学的あるいは経済学的には可能だが,少なくとも現在の会計検査,あるいはその国会報告のスタイルには適合しないというのが実際のところであろう。しかしながら,将来の検査報告のあるべき姿まで考えてみるならば,そういった分析についての理解を深めておくことは必要だと考える。
筆者は,このような問題意識から,上記の国内留学における修士論文で,農業政策が農家の農業生産コストに与えてきた影響を現実のデータを用いて分析しようと試みた。いま論文を読み直してみても実に不十分な分析ではあるが,結論は少々興味深いものとなった。論文全体を説明するスペースはないが,その主要な部分を,こうした分析と会計検査の関わりを考えて頂くためにも,その不十分であった部分も含めて,以下でできるだけ分かりやすく説明してみたい。
Ⅰ 分析方法
筆者が行った研究を一言でいうと次のようになる。
「現実のデータから農家の可変費用関数を推定し,その結果を用いて農業生産構造のいくつかの特徴を明らかにすると共に,『農業政策』が農業生産構造に与えてきた影響を考察した。」
まずこの文章の内容を説明することから始めたいと思う。
1 「可変費用関数」について
(1) 生産関数
ある人が米を生産して売ろうと考えたとする。米を生産するには,水田,水,モミ,肥料その他様々な生産資材が必要となる。また,田植え,草取り,刈り取りなどのために労働力も必要である。このように生産に必要なものは「生産要素」と呼ばれる。今,問題を簡単にするため,生産要素は「生産資材」と「労働力」の二つだけだとしよう。生産資材の量をK,労働力の量をLで表すことにする。
今,例えばK=100,L=100である時に,最も効率的に生産して米が100俵とれるとする。同様に,様々なK,Lの値に応じて,最も効率的に生産したときにとれる米の量がわかる。このようにして得られる,米の量(以下Qとする。)とK,Lの関係を「生産関数」と呼ぶ。この場合,生産関数は
Q =f(K, L)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・<1>
というように書かれる。「KとLがわかると,"f"という計算機を使ってQが求められる。」という意味である。"f"という計算機がどういう計算をしているかはまだわからない。ここでは次のような形である,と考えておく
Q=K×L÷100・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・<2>
K=100, L=100ならQ=100である。KかLのどちらかが0ならQも0となる。働かなければモノはできない,材料がなければモノは作れない,といったところであろうか。
この形をグラフに書くとグラフ1のようになる。曲線A1,A2,A3はそれぞれ米を100俵,200俵,300俵作るのに必要なKとLの組合せを表している。

(2) 費用関数
今,米を100俵作りたいとする。「生産資材」1セットは1,000円,「労働力」は1時間500円としよう。最も安上がりな作り方をしたら,費用はいくらかかるであろうか。
グラフ2を見て頂きたい。曲線Aは,先ほどの例の,米を100俵作るのに必要なKとLの組合せを示している。直線B1の下の斜線部分は10万円で買えるKとLの組合せを表している。曲線Aが直線B1よりも上にあるということは,10万円では米100俵は作れない,ということである。
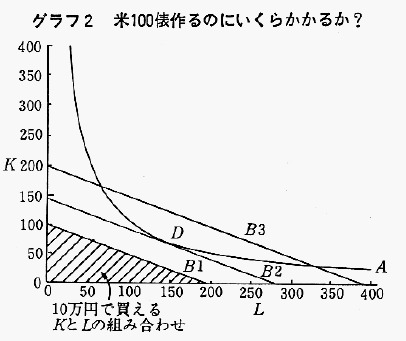
直線B3の下側の部分は20万円で買えるKとLの組合せを表しているが,曲線Aはこの部分を通過している。つまり,20万円あれば米100俵は作れるのだ。直線がもう少し下にあっても米100俵作ることができるのが御分かり頂けると思う。直線は下にあるほど,より安い費用で買えるKとLの組合せを表しているので,米100俵はもっと安い費用で作れることがわかる。
直線B2を見て頂きたい。曲線Aと点Dで接しているのだから,点Dで表されるKとLの組合せを用いれば米100俵を作ることができる。これ以上直線が下にあったら,もう米100俵は作れない。つまり点Dが「最も安く米100俵を作る」ことができるKとLの組合せを示す点なのである。
きちんと計算すると,このとき
L=141.4, K=70.7
となり,費用は合計141,421円となる。このように生産者が自分の生産関数を理解しているなら,生産量と生産要素の価格が決まるとその生産に要する最小の費用Cが決まる。生産関数の時と同じように,次のように書くことにする。
C=g(Q, PK, PL)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・<3>
PK,PLはそれぞれKとLの価格である。つまり生産量と生産要素の価格を"g"という計算機にかけると費用Cがわかる,というわけである。
この費用関数は,実は次のように定義される。
C=g(Q, PK, PL)
≡min(K,L)PK・K+PL・L
s.t. f(K, L)≧Q・・・・・・・・・・・・・・・・・・・・・・・・・・<4>
「min(K, L)PK・K+PL・L」というのは,KとLを自由に変化させたときにPK・K+PL・L(つまり生産に要する費用)がとり得る最小値,ということである。これだけなら,PK, PL, K, Lは普通すべて0以上の値をとるので,
K=L=0のときPK・K+PL・L=0・・・・・・・・・・・・・・・・・・・・・・・・・<5>
で最小となる。つまり,何も作らなければ費用はかからない,ということである。ところが,
s.t. f(K, L)≧Q
という式が付随している。「s.t.」とは,「制約条件」を表す。つまり,これは,「そのKとLを用いて最も効率的に生産を行ったとき,その生産量はQ以上でなければならない」ということを表している。つまり<4>は,全体としては「KとLの価格が各々PK,PLであるとき,生産量Qを確保することが可能なKとLの組合せを購入するのに必要となる最小限の費用」を意味しているのであり,これが即ち「費用関数」というわけである。
(3) 可変費用関数
今までは生産要素はK,Lの二つだけ,と考えていた。もう少し細かく分類してみよう。
L:労働量
M:機械の使用量
I:肥料,農薬などの投入量
O:動物,種苗などの投入量
K:耕地面積
費用関数では価格が用いられるのでそれぞれの価格を考え,各々PL,PM,PI,PO,PKとする。
すると費用関数は次のようになる。
C=g(Q, PL, PM, PI, PO, PK)・・・・・・・・・・・・・・・・・・・・・・・・・<6>
農家の実情を考えると,耕地の売買や貸借が十分行われているとは思われない。このような場合,耕地を「固定的生産要素」と考えて,次のように考えた方が正しい結果が得られる可能性が高くなる。
CV=g(Q, PL, PM, PI, PO, Z)・・・・・・・・・・・・・・・・・・・・・・・<7>
ただしZ:農家の保有耕地面積
CVは全費用から土地使用による費用を差し引いたもので可変費用と呼ぶことにする。式の右側にはPK(耕地の使用価格)の代わりにZ(農家の保有耕地面積)が含まれている。<3>式が<4>のように定義されるのと同様に,<7>式は
CV=g(Q, PL, PM, PI, PO, Z)
≡min(L, M, I, O)PL・L+PM・M+PI・I+PO・O
s.t. f(L, M, I, O, K)≧Q
-K≧-Z・・・・・・・・・<8>
と定義される。<4>との,生産要素を細分化した以外の違いは,最小化すべき費用から土地使用に係る部分が除かれていること及び利用できる耕地の面積がZまでに制限されていることの2点である。
さて,100戸の農家があるとしよう。その耕地面積はすべて同じ,生産要素価格は常に一定だとする。すべての農家が100俵の米を生産したとすると,その費用は全農家で同じであろうか?そんなはずはない。当然のことだが,費用の多少はこの式には出てこない数多くの要素に影響される。天候,家族構成,・・・。筆者はそれらのうち,費用に対する影響が大きく,またその効果に興味がもたれるもので,なおかつデータが利用できるもの二つを可変費用関数の式に含めた。
CV=g(Q, PL, PM, PI, PO, Z, G, t)・・・・・・・・・・・・・・・・・・・<9>
Gは農業政策がどの程度行われているかを示す指標である。筆者は農家一戸当りの,地方自治体の農業に対する財政支出額を用いた。tは時間を表す。農業技術は時間の経過に伴って変化していくと考えたのである。Gが可変費用関数に影響を与える経路はいろいろ考えられるが,ここでは次のように考えておく。
CV=g(Q, PL, PM, PI, PO, Z, G, t)
≡min(L, M, I, O)PL・L+PM・M+PI・I+PO・O
s.t. f (L, M, I, O, K, G, t)≧Q
-K≧-Z・・・・・・・・・・<10>
つまり,例えば研究開発,普及改良,社会資本の整備,各種指導などのように生産関数をシフトさせる働きを持つ,とするのである。この<10>式が,本論の実証分析で用いられる「モデル」ということになる。
ここまでのところを簡単にまとめてみよう。
① 農家が最も効率的に生産しているなら,「生産関数」によって生産要素の量から生産量を計算できる。
② 農家が自分の生産関数を知っていて,安上がりに生産しようと努力していれば,「費用関数」によって生産量と生産要素価格から生産の費用を計算できる。
③ この論文で用いる可変費用関数は次のような形をしている。
CV=g(Q, PL, PM, PI, PO, Z, G, t)
つまり,農家の可変費用は生産量及び土地以外の生産要素価格のほか,農家の保有耕地面積,農家が属する自治体の,農家一戸当りの農業に対する財政支出,時間などの要因に影響されるとする。
2 「農業生産構造の特徴」について
ここでは「平均可変費用」,「限界費用」,「規模の経済」といった,生産構造の特徴を表す指標について説明する。
今,式<9>の右側に出てくる変数のうち生産要素価格,耕地面積,自治体の財政支出,時間が一定であると考えよう。このとき可変費用と生産量の関係は普通,グラフ3のaのようになると考えられる。
平均可変費用(AC)は米1俵当りの可変費用のことで
AC=CV÷Q・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・<11>
である。これが米の価格を上回れば当然赤字となる。
「限界費用」は経済学では重要な概念で,これは「現在の生産量をあと1単位増加させるときに余分に必要となる費用」のことである。例えば100俵作っているときの限界費用(MC)は
MC=(101俵作るための費用)−(100俵作るための費用)・・・・<12>
である。これは,CVのグラフ(グラフ3のa)の傾き,ともいえる。CV,AC,MCの関係はグラフ3のようになる。

グラフ3のbを見て頂きたい。今,米の価格はP円だとする。
生産量がQ1だと,P>MCとなる。生産量を1俵増大させると費用はMC,収入はP円増加する。P>MCであるから収入増は費用増よりも大きく,利益は増大する。
生産量がQ3だと,P<MCとなる。生産量を1俵減少させると費用はMC,収入はP円減少する。P<MCであるから収入源より費用源が大きく,従って利益は増大する。
生産量がQ2だとP=MCとなる。生産量を増大しても減少しても利益は増加しない。このとき,農家の利益は最大になっているのである。
「規模の経済(RTS)」とは,全生産要素の投入量を1%増大させたとき生産量は何%増加するか,という数字である。これが1より大きければ生産量を増大させた方が,1より小さければ生産量を減少させた方が生産が「経済的」になるわけである。
3 「推定」等について
筆者は,分析の対象とした全農家が上記の可変費用関数に従っている,と仮定した。そして現実のデータから可変費用関数の具体的な姿を「推定」し,さらに推定された可変費用関数を用いていろいろな計算を行ったのである。
(1) 「推定」
ある学者が次のように考えたとしよう。「平均寿命はその人が1日平均何本のタバコを吸うかで決まる。」平均寿命をY,1日当りの平均喫煙量をXとすると,上の文章は次のような関数があるということを表している。
Y=h(X)・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・<13>
彼は"h"という計算機は具体的には次のような形をしていると考えた。
Y=aX+b
彼はaとbの値を知りたい。このようなとき,現実のデータを用いて,次のような方法でaとbを「推定」することができる。
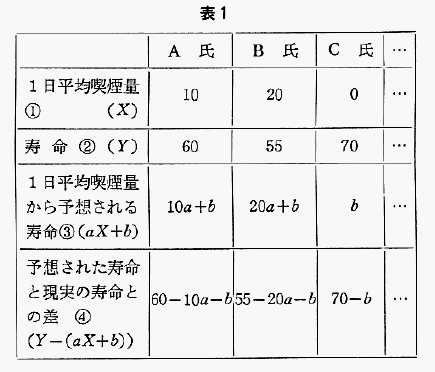
表1を見て頂きたい。A氏,B氏,C氏,・・・のことを「標本」という。③の具体的な数値は,aとbがまだ不明なので明らかでない。④は予想と現実の「ずれ」である。この「ずれ」が小さいほど良い予想だ,といえる。そこで,この「ずれ」が全体として最も小さくなるようなaとbを捜すことになる。ただし④はプラスになったりマイナスになったりするので,普通これを二乗したものを全標本について合計したものが最小になるようにする。
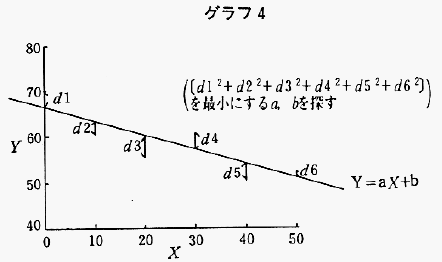
グラフで考えるとつぎのようになる(グラフ4)。
各々のデータから,直線Y=aX+bに対して,Y軸に平行な線分を引く。その線分の長さを二乗してその和を求める。この数字が最小になるようにaとbを決めるのである。この方法は「最小二乗法」と呼ばれる。二つだけ,注意すべき点を述べておこう。
① これはXとYの「関係」を表しているもので必ずしも「因果関係」を表しているとは限らない。
② 推定に用いた関数型(今の例ではY=aX+b)が正しくないと,正しい結果が出ないことがある。
この2点から,前述したような,推定に用いる「モデル」及びその関数型の決定が非常に重要になってくるのである。
なお,筆者が推定に用いた関数型はトランスログ型(注1)と呼ばれるものである。また推定方法は3段階最小二乗法(注2)を用いた。
(2) 推定結果を用いた計算
上の例で,仮に
a=-0.5 b=70
だったとしよう。これは簡単にいってしまえば「人はタバコを吸わなければ70歳ぐらいまで生きられるが,1日平均1本吸うごとに0.5歳ずつ寿命が縮まる」という意味である。つまり推定された「寿命関数」を用いてタバコが人の寿命に与える影響を考察することができたのである。
これと同様にして筆者は推定された「可変費用関数」を用いて前述した「平均可変費用」「限界費用」「規模の経済」などを計算すると共に,"G"がそれらに与えてきた影響をも計算したのである。
Ⅱ データ
分析に用いた標本は,昭和49〜60年の,東北・北関東計9県の平均農家で,計108になる。
農業に対する財政支出以外のデータはすべて農林水産省が毎年刊行している『農家経済調査報告』及び『農村物価賃金統計』から得た。
"G",即ち農業に対する財政支出は,前にも少々述べたが,自治省が毎年刊行している『地方財政統計年報』から得た各年の,各県およびその県内の市町村等が支出した農業費・農地費・畜産業費の合計(これは純計値とはなっておらず,二重計上となっている部分があるという問題点があるが,他に適切なデータが見つけられなかったためこのまま使用した。)を,農林水産省が毎年刊行している『ポケット農林水産統計』による各年・各県の農家数で除したもの(以下「地方自治体の財政支出」と呼ぶ。)を用いた。従って,国の直轄事業費,試験研究費などは含まれておらず,「国の農業政策」という本来の興味の対象に対して間接的なアプローチになってしまうという難点はあるが,国の農業予算に占める補助金等の比率の高さ及び地方公共団体の農業政策や農業予算における国の農業政策や補助金等の重要性等を考えれば次善の策として許されるのではないか,という判断でこれを用いることとした。
以下の分析では,上記のようにして得られたいわゆる「生データ」を,さらに加工したものも用いられている。
Ⅲ 分析結果
以下で述べる部分は,「実証分析」,つまり実際のデータと計量経済学的(または統計学的)手法を用いて理論モデルが正しいかどうかを実証的に確認している部分に当たる。実際にはそれ以前に,「理論分析」として,簡単な理論モデルを用いて財政支出が農業生産及びその費用に与える影響を考察した。この理論モデルは,基本的には<10>式とほぼ同じである(注3)。これに様々な仮定(注4)を設け,非線形計画法(注5)の定理を用いて比較静学的分析(注5)を行った。ここでは分析で得られた結論の一部だけを簡単に述べるにとどめるが,財政支出が農家の生産関数を下方にシフト(平たく言えば,同じだけの米を作るのに余計に生産資材や労働力が必要となること)させる場合,農家の平均費用及び限界費用を増大させることもありうるという結果が得られた。少し考えて頂けば,容易に理解して頂けるものと思う。実際にそんなことがあるものか,とお考えの方もおられるかもしれないが,水田を転作して大豆畑にしたが,米に比べて大豆の方が生産効率が悪い,といった場合を考えれば,ありえないことではない。
もうひとつ,念のため説明しておくと,いままで説明してきた,生産関数や費用関数を用いた分析は,ミクロ経済学,つまり生産者・企業,消費者といった,ひとつひとつの経済主体の行動を分析する経済学で用いられる手法である。(なお,「マクロ経済学」と言うのは,あるひとつの国や地域などに着目し,その中の経済活動全体の動きを分析する経済学である。)一方,私が始めに述べた「ミクロ的な視点から行われている検査」,「マクロ的視点から行われている検査」という表現の意味は,それぞれ検査を,前者は,ひとつひとつの経理や事業に着目して行う(例:工事の出来形検査),後者は,ある政策(に伴う支出)とその効果全体について着目して行う(例:政府の農業政策の効果の分析),ということである。つまり,ここでの私の分析は,「マクロ的な視点から」「ミクロ経済学の手法を用いて」(さらに言うなら「マクロ的データを用いて」)行ったものだということになる。
「実証分析」を始めたい。まず簡単に主要なデータの動きを見てみよう。以下で用いる数値は,各データを,年ごとに平均したものである。
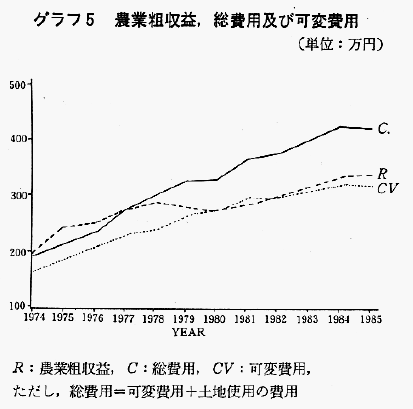
グラフ5は農業粗収益,総費用,可変費用を比較したものである。51年までは農業粗収益が総費用を上回っていたが,それ以後の費用の上昇に対して農業粗収益は伸び悩み,55年以降はやっと可変費用を賄える,といった水準になっていることがわかる。
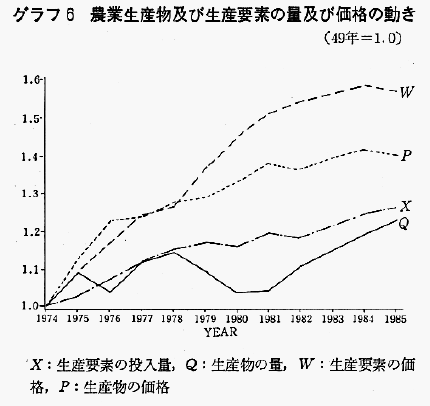
グラフ6は,生産物,生産要素それぞれの量と価格の指数の動きを示したものである。54年以降,生産要素の投入量水準と比べて生産量水準が停滞している。53年に開始された水田利用再編対策によって減反が強化されたことや54年以降の牛乳の計画生産が影響しているように思える。一方,価格水準は,53年秋の石油ショックの影響か,54年以降生産要素価格が生産物価格より相対的に高い水準にある。
グラフ7は「地方自治体の財政支出」の動きを示している。55年までは大きく伸びていたが,それ以後は頭打ちになっていることがわかる。

では,本格的な分析を始めよう。以下の数値は,各変数を,年ごとに各県の農家数で加重平均して計算したものである。
まず推定された平均可変費用及び限界費用(注6)と生産物価格を比較してみる(グラフ8)。常に「生産物価格>平均可変費用>限界費用」となっている。

限界費用が生産物価格より低いということは,先ほども述べたように生産量を増加させれば利益が増えるということである。それが行われていないということは何らかの外からの力で生産量が最適な水準よりも低く抑えられていることを示唆している。
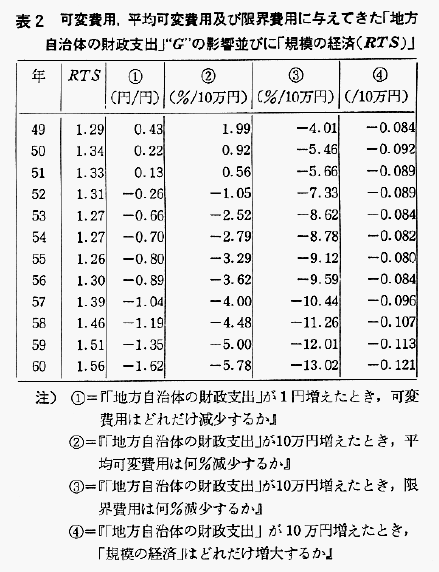
表2をみると一貫してかなり大きな「規模の経済」(注7)が存在していることがわかる。特に55年以降,急激に上昇している。
「地方自治体の財政支出」"G"が費用にどのような影響を与えてきたかをみてみよう(注8)。
表2の①の数値は,例えば49年においては,「地方自治体の財政支出」の1円の増加は可変費用の0.43円の減少をもたらした,という意味である。52年以降,「地方自治体の財政支出」の増加は可変費用を増大させた,という結果になっている。
②は52年以降,③は49年以来常に負の値をとっており,「地方自治体の財政支出」の増加は常に限界費用を,また52年以降は平均可変費用をも,増大させる働きをしてきたことになる。この傾向は時間の経過と共にますます悪化している。
④は49年以来常に負の値をとっており,「地方自治体の財政支出」の増加は,常に「規模の経済」を低下させる働きをしてきたことが読み取れる。特にその傾向は55年以降急激に強まっている。
Ⅳ まとめ
今までの分析で得られた結果が意味するところを考えてみよう。まず,分析結果を要約してみる。
はじめに費用関数の推定結果を用いて生産構造のいくつかの特徴を明らかにしたところ,限界費用が平均可変費用・生産物価格の双方を下回っていること,かなり大きな「規模の経済」が存在していることなどが明らかになった。さらに,「地方自治体の財政支出」が与えてきた影響を分析した。その結果,「地方自治体の財政支出」は49年以来限界費用を,52年以降は可変費用及び平均可変費用をも増大させる方向に機能してきたという結果となっていることがわかった。また,49年以来「規模の経済」を縮小させる働きを持っていたことも明らかになった。
今までの分析の範囲内で考える限り,農業に対する財政支出は農業生産構造に対して望ましくない方向に機能してきたと言わざるを得ない。可変費用・平均可変費用・限界費用を増大させてきたということは,生産性を低下させ,輸入農産物に対する価格競争力を低下させてきたということである。「規模の経済」を低下させる,ということは大規模生産のメリットを減らし,生産規模拡大の意欲を失わせ,それを抑制してきた,ということになるであろう。つまり,農業に対する財政支出は,生産性の向上,経営規模拡大,自立経営農家の育成といった農業基本法の理念と反対方向へのインパクトを農業生産構造に与えてきたように思われるのである。
ここで,以上で行った分析の限界について述べておきたいと思う。
最も重要な事は,農業に対する財政支出の実際の効果のうち,この研究で用いた方法で分析されるのはその一部分に過ぎないということである。例えば生産量の変化をもたらす財政支出の効果,あるいは土地の流動化を通じて規模拡大を促進しようとする政策や減反のように逆に実質的な耕地面積を減少させようとする政策の効果は,「生産量の変化による効果」及び「経営耕地面積の変化による効果」としてしか捉えられない。また,「地方自治体の財政支出」というデータを用いていることを考えれば,国の直轄事業等の財政支出による効果も捉えられない。上で述べた分析結果を読むときにはこれらのことを念頭に置いておく必要がある。
ところで,分析の結果かなり大きな「規模の経済」が存在していることがわかった。これは,1農家当りの生産量を増大させ,それに合わせて耕地面積をも拡大させることができれば,平均費用を大幅に減少させることが可能だということである。しかも限界費用は生産物価格よりも低い水準にあるので,生産量の増大は農家の利益も増大させる。従って,農家単位で考えれば「経営規模拡大による自立経営農家の育成」という政策理念は現在でも通用するものだといえる。それによって安い農産物と健全な農業経営を両立させることができるかも知れない。
それが現実化しなかったのは,労働節約的な技術進歩と価格支持政策のおかげで中小兼業農家が農地を手放さずにすみ,規模拡大が行われなかったためであろう。政府としても兼業農家の「切り捨て」となる政策は実行しにくく,価格政策等を通じて兼業農家の増加に手を貸してきた面もある。しかし,現実に採られた政策は,この分析の範囲では,逆に国内農業にとって悪い方向に機能してきたように見える。思い切った政策の転換を行うべきではないだろうか,と言うのが研究を終えた筆者の感想である。
Ⅴ 最後に
経済学に親しんでいない方々には少々難解だったかも知れないが,「マクロ的視点からの分析が,統計学的あるいは経済学的には可能だが,少なくとも現在の会計検査,あるいはその国会報告のスタイルには適合しない」という意味がご理解頂けたであろうか。とはいっても,いままで行ってきた分析におけるような問題意識が会計検査において重要であること,そしてその重要度がこれからますます高くなっていくであろうということは間違いないと思う。その問題意識をどの様に検査に反映していくかが,これからの我々会計検査院職員の課題であろう。この論文はそのような課題に筆者なりに取り組んだひとつの試みであるが,筆者の勉強不足のため不正確な表現が随所に見受けられるかも知れない。力不足をお詫びするとともに,読者諸氏の遠慮のない御指摘及び御教示をお願いして,筆を置くこととしたい。




参考文献
Chiang, A. C. Fundamental Methods of Mathematical Economics, 3rd ed. McGraw-Hill Book Co., 1984
Henderson, J. M. and Quandt, R. E. Microeconomic Theory, 3rd ed. McGraw-Hill Book Co., 1980
自治省『地方財政統計年報』。
Johnston, J. Econometric Methods, 3rd ed. McGraw-Hill Book Co., 1984
Kuroda, Y. "The Production Structure and Demand for Labor in Postwar Japanese Agriculture, 1952-82." Amer. J. Agr. Econ. 69(1987a) : p328-337
Kuroda, Y. "Impacts of Economies of Scale and Technological Change on Agricultural Productivity in Japan. " Discussion Paper No. 323. Institute of Socio-Economic Planning, University of Tsukuba, Ibaraki, Japan, 1987 b
丸山義皓『企業・家計複合体の理論』創文社,1984年
農林水産省『昭和59年度農業白書附属統計表』,1985年
農林水産省『農家経済調査報告』
農林水産省『農村物価賃金統計』
農林水産省『ポケット農林水産統計』
鈴土靖「農業政策の効果の計量分析」筑波大学大学院修士論文,1988年
Varian, H. R. Microeconomic Analysis, 2nd ed. W. W. Norton & Co., 1984